Predicting House Prices – Project 3
1) The dataset¶
This Kaggle competition involves using the Ames Housing dataset to predict house prices using a large array of variables.
This is pre-split into a training set and testing set with the caveat being that the only way to score my predictions using the test set is to submit the predictions to the Kaggle competition.
According to Kaggle:
Submissions are evaluated on Root-Mean-Squared-Error (RMSE) between the logarithm of the predicted value and the logarithm of the observed sales price. (Taking logs means that errors in predicting expensive houses and cheap houses will affect the result equally.)
I intend to experient with 3 different methods:¶
- 1) Use all of the variables
- Use the numerical data as is
- Convert the ones I can into numerical variables and give each one a unique value
- deal with missing values
- remove collinearity
- 2) Trying stepwise regression and using only features with the highest impact
- impute all using most frequent
- one-hot encoding every feature
- remove all remaining non numeric features
- remove collinearity
- 3) Simply Factorizing (turning all categorical into numbers)
2) What is regression and how does it work?¶
Explain what regression is and how it works (specifically linear regression, as we have covered it in class). Bonus points for math (up to 5 bonus points for very good explanations).¶
Linear regression generalizes variables to calculate an output. It takes one or more variables with coefficients and constant(s) as a function and using this you can ‘predict.’ These are great when some factor has a relationship with another. For example, an easy visualization is with students: the more higher they score on tests, the higher their final exam grade will be. One could include many variables alongside this such as attendance, homework grades and quiz grades. However, this may be tricky when trying this with calculating final grades. There is linear dependence between test and quiz grades and the final grade of a class, at least when you include all grades.
There are 5 assumptions that must be made when performing linear regression:
- All variables are independent of one another (no multicollinearity)
- There is a linear relationship them (they are related)
- Resisudal errors should be normally distributed
- All observations are independent (the value of a single occurance should not depend on another)
- There are no missing values
There are 2 main statistics to look at after running this model:
- r2, the coefficient of determination, represents the percentage of variation that your dependent variable can be explained by your independent variable(s). The closer this value is to 1 the better your data variation can explain your results.
- and RMSE, Root Mean Square Error, which represents how well a model is able to fit the dataset. The closer this value is to 0 the better.
Work in progress
3) Experiment 1: Data understanding¶
Before diving right into the work, what steps do you take to first gain an understanding of your data? For example, are any features correlated with each other? Are there any existing patterns? What visualizations can you make to help gain this initial understanding?¶
Package pre-reqs:
- Pandas for loading and manipulating the csv files
- sklearn for statistical analysis
- seaborn for fancy plots and charts
import pandas as pd
import seaborn as sns
import numpy as np
from collinearity import SelectNonCollinear # https://github.com/gianlucamalato/collinearity
from sklearn.feature_selection import f_regression
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.impute import SimpleImputer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# Let's disable warnings to make this prettier for posting
import warnings
warnings.filterwarnings('ignore')
# Apparently... the default format 'retina' breaks the html for my website.
# my options are... 'jpg', 'png', 'svg', 'pdf', and 'retina'.
# retina size: 196k
# jpg: 146k
# png: 186k (doesn't work)
# svg: 161k (doesn't work)
# pdf: 62k (doesn't work)
%config InlineBackend.figure_format ='jpg'
To get started, we first must load our dataset
house_df = pd.read_csv('data/train.csv')
test_df = pd.read_csv('data/test.csv')
house_df.shape
(1460, 81)
1460 entries and 81 variables!¶
house_df.describe()
| Id | MSSubClass | LotFrontage | LotArea | OverallQual | OverallCond | YearBuilt | YearRemodAdd | MasVnrArea | BsmtFinSF1 | … | WoodDeckSF | OpenPorchSF | EnclosedPorch | 3SsnPorch | ScreenPorch | PoolArea | MiscVal | MoSold | YrSold | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 1460.000000 | 1460.000000 | 1201.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1452.000000 | 1460.000000 | … | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 | 1460.000000 |
| mean | 730.500000 | 56.897260 | 70.049958 | 10516.828082 | 6.099315 | 5.575342 | 1971.267808 | 1984.865753 | 103.685262 | 443.639726 | … | 94.244521 | 46.660274 | 21.954110 | 3.409589 | 15.060959 | 2.758904 | 43.489041 | 6.321918 | 2007.815753 | 180921.195890 |
| std | 421.610009 | 42.300571 | 24.284752 | 9981.264932 | 1.382997 | 1.112799 | 30.202904 | 20.645407 | 181.066207 | 456.098091 | … | 125.338794 | 66.256028 | 61.119149 | 29.317331 | 55.757415 | 40.177307 | 496.123024 | 2.703626 | 1.328095 | 79442.502883 |
| min | 1.000000 | 20.000000 | 21.000000 | 1300.000000 | 1.000000 | 1.000000 | 1872.000000 | 1950.000000 | 0.000000 | 0.000000 | … | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 1.000000 | 2006.000000 | 34900.000000 |
| 25% | 365.750000 | 20.000000 | 59.000000 | 7553.500000 | 5.000000 | 5.000000 | 1954.000000 | 1967.000000 | 0.000000 | 0.000000 | … | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 5.000000 | 2007.000000 | 129975.000000 |
| 50% | 730.500000 | 50.000000 | 69.000000 | 9478.500000 | 6.000000 | 5.000000 | 1973.000000 | 1994.000000 | 0.000000 | 383.500000 | … | 0.000000 | 25.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 6.000000 | 2008.000000 | 163000.000000 |
| 75% | 1095.250000 | 70.000000 | 80.000000 | 11601.500000 | 7.000000 | 6.000000 | 2000.000000 | 2004.000000 | 166.000000 | 712.250000 | … | 168.000000 | 68.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 8.000000 | 2009.000000 | 214000.000000 |
| max | 1460.000000 | 190.000000 | 313.000000 | 215245.000000 | 10.000000 | 9.000000 | 2010.000000 | 2010.000000 | 1600.000000 | 5644.000000 | … | 857.000000 | 547.000000 | 552.000000 | 508.000000 | 480.000000 | 738.000000 | 15500.000000 | 12.000000 | 2010.000000 | 755000.000000 |
8 rows × 38 columns
We really don’t want or need the Id column for predictions
#del house_df['Id']
I will not name all of the variables, I will however describe some that I believe will be the most important (we’ll find out soon!)
- MSZoning (categorical): Identifies the general zoning classification of the sale.
- LotArea (continuous): Lot size in square feet
- Neighborhood (categorical): Physical locations within Ames city limits
- OverallQual (ordinal): Rates the overall material and finish of the house
- 1stFlrSF: First Floor square feet
Let’s see if we can find some patterns! First a correlation heatmap
# Let's set the default plot size
sns.set(rc={"figure.figsize":(30, 15)})
sns.set(rc={"figure.dpi": 75})
sns.heatmap(house_df.corr(), cmap="YlGnBu", annot=True, fmt='.1g') # The website cannot handle the default 'retina' format, nor 'png' and 'svg.' Only 'jpg.'
<AxesSubplot: >
This is a bit much, either way we know that some variables are highly correlated with others. If we’re looking for relationships to the target, SalePrice then we know that the following are highly related:
- OverallQual
- TotalBsmtSF
- 1stFlrSF
- GrLivArea
- GarageCars
- GarageArea
And these are just the ones with more than a 0.6 correlation.
Now let’s explore what variables are highly related to other variables using the 0.60 cutoff again:
- GarageCars and OverallQual
- GarageCars and GarageArea
- GarageYrBlt and YearBuilt (duh?)
- GarageYrBlt and YearRemodAdd
- TotRmsAbvGrd and GrLivArea
- 1stFlrSF and TotalBsmtSF (makes sense, usually basements are around the same size as the ‘ground’ floor)
With these in mind…
4) Experiment 1: Pre-processing¶
After the initial understanding, what steps need to be taken? Do you need to deal with null values? What features are you going to try using for your first experiment and why? Do you need to transform any features (e.g., change from categorical to numerical)? Are you trying to create any new features to use?¶
Let’s check for null values.
# Loop through each column
# and check the amount of nulls.
# Only print if there are more than 0.
for col in house_df.columns:
if house_df[col].isnull().sum() > 0:
print(f'{house_df[col].isnull().sum()} null values in {col}')
259 null values in LotFrontage 1369 null values in Alley 8 null values in MasVnrType 8 null values in MasVnrArea 37 null values in BsmtQual 37 null values in BsmtCond 38 null values in BsmtExposure 37 null values in BsmtFinType1 38 null values in BsmtFinType2 1 null values in Electrical 690 null values in FireplaceQu 81 null values in GarageType 81 null values in GarageYrBlt 81 null values in GarageFinish 81 null values in GarageQual 81 null values in GarageCond 1453 null values in PoolQC 1179 null values in Fence 1406 null values in MiscFeature
In a dataset with 1460 entries, it is unlikely that these variables with large amounts of null values will make a huge difference.
Let’s verify this with the matrix above comparing these variables with SalePrice:
- MiscFeature: N/A (categorical) cannot alter for linear regression.
- PoolQC: N/A (categorical) could perhaps convert this to an ordinal value. 1453 nulls.
- Alley: N/A (categorical) cannot alter for linear regression.
- Fence: N/A (categorical) could perhaps convert this to an ordinal value. 1179 nulls.
- FireplaceQu: N/A (categorical) could perhaps convert this to an ordinal value. 690 nulls.
- LotFrontage: 0.4 with 259 nulls.
I am only willing to convert FirePlaceQu (Fire place quality) to a numerical variable because it has fewer than half the total values missing. Let’s try it out.
Let’s convert all ordinal variables into numeric values.
I will use 1 as the highest quality with the higher the value the lower the quality is.
We will also delete these fields with a large number of NA values
def del_poor_features(df: pd.DataFrame):
df = df.drop(['Alley'], axis=1)
df = df.drop(['FireplaceQu'], axis=1)
df = df.drop(['PoolQC'], axis=1)
df = df.drop(['Fence'], axis=1)
df = df.drop(['MiscFeature'], axis=1)
return df
house_df = del_poor_features(house_df)
def convert_categorical_to_num(df:pd.DataFrame):
# General Shape of property. Regular, slightly irregular etc
df['LotShape'] = df['LotShape'].replace(to_replace=['Reg', 'IR1', 'IR2', 'IR3'], value=[1,2,3,4])
# Evaluates the quality of the material on the exterior. Excellent all the way to Poor
df['ExterQual'] = df['ExterQual'].replace(to_replace=['Ex', 'Gd', 'TA', 'Fa', 'Po'], value=[1,2,3,4,5])
# Evaluates the present condition of the material on the exterior. Excellent all the way to Poor
df['ExterCond'] = df['ExterCond'].replace(to_replace=['Ex', 'Gd', 'TA', 'Fa', 'Po'], value=[1,2,3,4,5])
# Evaluates the height of the basement. Excellent all the way to Poor. NA for no basement
df['BsmtCond'] = df['BsmtCond'].replace(to_replace=['Ex', 'Gd', 'TA', 'Fa', 'Po', 'NA'], value=[1,2,3,4,5,6])
# Refers to walkout or garden level walls. Good exposure all the way to no exposure and no basement
df['BsmtExposure'] = df['BsmtExposure'].replace(to_replace=['Gd', 'Av', 'Mn', 'No', 'NA'], value=[1,2,3,4,5])
# Rating of basement finished area. Good all the way to unfinished and no basement
df['BsmtFinType1'] = df['BsmtFinType1'].replace(to_replace=['GLQ', 'ALQ', 'BLQ', 'Rec', 'LwQ', 'Unf', 'NA'], value=[1,2,3,4,5,6,7])
# Heating quality and condition. Excelling to poor
df['HeatingQC'] = df['HeatingQC'].replace(to_replace=['Ex', 'Gd', 'TA', 'Fa', 'Po'], value=[1,2,3,4,5])
# Central air conditioning. N=0 1=Y
df['CentralAir'] = df['CentralAir'].replace(to_replace=['N', 'Y'], value=[0,1])
# Kitchen Quality. Excelling to poor
df['KitchenQual'] = df['KitchenQual'].replace(to_replace=['Ex', 'Gd', 'TA', 'Fa', 'Po'], value=[1,2,3,4,5])
# Evaluates garage quality. Excellent all the way to Poor. NA for no garage
df['GarageQual'] = df['GarageQual'].replace(to_replace=['Ex', 'Gd', 'TA', 'Fa', 'Po', 'NA'], value=[1,2,3,4,5,6])
# Evaluates garage condition. Excellent all the way to Poor. NA for no garage
df['GarageCond'] = df['GarageCond'].replace(to_replace=['Ex', 'Gd', 'TA', 'Fa', 'Po', 'NA'], value=[1,2,3,4,5,6])
# Paved driveway. paved=1, partial pavement=2, dirt/gravel=3
df['CentralAir'] = df['CentralAir'].replace(to_replace=['Y', 'P', 'N'], value=[1,2,3])
# Fence Quality. Good privacy to minimum to no fence
df['KitchenQual'] = df['KitchenQual'].replace(to_replace=['GdPrv', 'MnPrv', 'GdWo', 'MnWw', 'NA'], value=[1,2,3,4,5])
return df
house_df = convert_categorical_to_num(house_df)
Let’s check our collinearity again. Also since we’re only interested in numeric fields here let us update our df to reflect this. This will make our job easier down the line.¶
def exlude_non_num(df: pd.DataFrame):
df = df.select_dtypes(exclude=['object'])
return df
print(f"Shape before dropping NA: {house_df.shape}")
house_df = exlude_non_num(house_df)
house_df = house_df.dropna()
house_df = house_df.astype(np.float32)
print(f"Shape after dropping NA: {house_df.shape}")
Shape before dropping NA: (1460, 76) Shape after dropping NA: (1096, 49)
NA values and non-numerical values will cause issue when we try to reduce collinear fields¶
Dropping these problematic rows yeilds a 364 entry loss, or 24.9% of the previous df
##### This image makes the html too large for my website :( ###############################################################################################################3
sns.heatmap(house_df.corr(), cmap="YlGnBu", annot=True, fmt='.1g')
<AxesSubplot: >
Okay so it worked, there are more fields… now what? Well let’s get rid of some of this collinearity. I found a cool package called ‘collinearity’ and we’re gonna put it to use.¶
We must create a nonCollinar object, and I’m going to set the threshold to 0.4. That should be good enough for our regression right?¶
def rem_collinear_features(correlation_threshold: float, scoring, x_df: pd.DataFrame, y_df: pd.DataFrame):
selector = SelectNonCollinear(correlation_threshold, scoring=scoring)
selector.fit(x_df.to_numpy(), y_df.to_numpy())
mask = selector.get_support()
return pd.DataFrame(x_df.loc[:,mask],columns = np.array(x_df.columns)[mask])
# Now is as good a time as ever to create our x and y
x_house_df = pd.DataFrame(house_df)
del x_house_df['SalePrice']
y_house_df = house_df.SalePrice
Also, number of features before removing collinearity
print(x_house_df.shape[1])
48
x_house_df = rem_collinear_features(0.4, f_regression, x_house_df, y_house_df)
sns.heatmap(x_house_df.corr().abs(),annot=True,fmt='.2g')
<AxesSubplot: >
And number of features after removing collinearity
print(x_house_df.shape[1])
26
Down to 25 features! Hopefully these are the most impactful.
Also we’re going to try a pairwise plot so we can try to identify trends
# pairplot = sns.pairplot(data=x_house_df)
Truth be told, I wish that were useful but there are too many fields at this time.
What would be useful though is a list of final features.
final_features = x_house_df.columns
4a) Experiment 1: Modeling¶
Create a linear regression model for your first experiment.¶
Documentation: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html
Creating our first linear model object¶
lr1 = LinearRegression(n_jobs=-1)
Let’s jump straight into it. Let’s fit it and score it!
In order to do this, we’ll split this into a 20/80 test/train split
x_train, x_test, y_train, y_test = train_test_split(x_house_df, y_house_df, shuffle=True, test_size=0.2, random_state = 11)
lr1.fit(x_train, y_train)
LinearRegression(n_jobs=-1)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression(n_jobs=-1)
4b) Experiment 1: Evaluation¶
Evaluate your first model. For example, use root mean squared error (RMSE).¶
Note: if you would like to try submitting your work to the competition, their submissions are evaluated using RMSE. Submitting to the competition is not required, but it might be fun to experience! More information on how to submit is under the "Overview" tab, then "Evaluation."
predictions = lr1.predict(x_test)
r2 = r2_score(y_test, predictions)
rmse = mean_squared_error(y_test, predictions, squared=False)
print(f'{r2} r^2 score')
print(f'{rmse} RMSE score')
0.730429387411119 r^2 score 44227.64453125 RMSE score
An r2 score of 0.73. Wow 73% is better than I expexted. That is how well our dependent variable can be explained by the model using our independent variables.
Let’s get the test csv set up to be scored by Kaggle¶
First, how many are we predicting?
test_df.shape[0]
1459
1459!
test_df = del_poor_features(test_df)
test_df = convert_categorical_to_num(test_df)
test_df = exlude_non_num(test_df)
test_df = test_df[final_features]
Okay, so these missing values are going to mess with us and this time we can’t simply drop them because we need all 1459 to get the best score possible. So we’ll use sklearns imputing abilities and try out filling in the values with mean, median or most_frequent.¶
imputer = SimpleImputer(missing_values=np.nan, strategy='mean')
imputer.fit(test_df)
SimpleImputer()In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
SimpleImputer()
test_df = imputer.transform(test_df)
test_df = test_df.astype(np.float32)
test_df = pd.DataFrame(test_df, columns = final_features)
Okay…let’s predict then set up the csv.¶
It should be formatted: Id,SalePrice
to_kaggle_predictions_1 = pd.Series(data = lr1.predict(test_df), dtype=np.float32, name = 'SalePrice')
to_kaggle_predictions_1
0 139145.7500
1 29987.5625
2 166254.8125
3 202686.9375
4 212489.6875
...
1454 39162.0625
1455 50228.9375
1456 173229.8750
1457 105499.4375
1458 258649.4375
Name: SalePrice, Length: 1459, dtype: float32
to_kaggle_predictions_1 = pd.concat([test_df['Id'],to_kaggle_predictions_1], axis=1)
to_kaggle_predictions_1['Id'] = to_kaggle_predictions_1['Id'].astype(np.int32)
to_kaggle_predictions_1.head()
| Id | SalePrice | |
|---|---|---|
| 0 | 1461 | 139145.7500 |
| 1 | 1462 | 29987.5625 |
| 2 | 1463 | 166254.8125 |
| 3 | 1464 | 202686.9375 |
| 4 | 1465 | 212489.6875 |
We’ve done it! Let’s score this thing up.¶
to_kaggle_predictions_1.to_csv('submissions/to_kaggle_predictions_1.csv', index=False)
Kaggle has given me a score of 0.98067
That’s good I think?
Welp, I’m in place 3882 out of ~4000 sooooo
Yeah, looks like a score closest to zero is best. Let’s work on that!
Preprocessing:¶
Reset back to our starting position
house_df = pd.read_csv('data/train.csv')
Step 1: impute all features using the most frequent value. AKA replace all missing values with the most common value¶
+ impute all using most frequent
+ one-hot encoding every feature
+ remove collinearity
print(f'{house_df.isnull().sum().sum()} total null values before imputing')
6965 total null values before imputing
imputer = SimpleImputer(missing_values=np.nan, strategy='most_frequent')
imputer.fit(house_df)
SimpleImputer(strategy='most_frequent')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
SimpleImputer(strategy='most_frequent')
house_df = pd.DataFrame(imputer.transform(house_df), columns = house_df.columns)
for col in house_df.columns:
if house_df[col].isnull().sum() > 0:
print(f'{house_df[col].isnull().sum()} null values in {col}')
if house_df.isnull().sum().sum() == 0:
print("No missing values!")
else:
print(f"{house_df.isnull().sum().sum()} values still remain")
No missing values!
No missing values now!¶
house_df.describe()
| Id | MSSubClass | MSZoning | LotFrontage | LotArea | Street | Alley | LotShape | LandContour | Utilities | … | PoolArea | PoolQC | Fence | MiscFeature | MiscVal | MoSold | YrSold | SaleType | SaleCondition | SalePrice | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 1460 | 1460 | 1460 | 1460.0 | 1460 | 1460 | 1460 | 1460 | 1460 | 1460 | … | 1460 | 1460 | 1460 | 1460 | 1460 | 1460 | 1460 | 1460 | 1460 | 1460 |
| unique | 1460 | 15 | 5 | 110.0 | 1073 | 2 | 2 | 4 | 4 | 2 | … | 8 | 3 | 4 | 4 | 21 | 12 | 5 | 9 | 6 | 663 |
| top | 1 | 20 | RL | 60.0 | 7200 | Pave | Grvl | Reg | Lvl | AllPub | … | 0 | Gd | MnPrv | Shed | 0 | 6 | 2009 | WD | Normal | 140000 |
| freq | 1 | 536 | 1151 | 402.0 | 25 | 1454 | 1419 | 925 | 1311 | 1459 | … | 1453 | 1456 | 1336 | 1455 | 1408 | 253 | 338 | 1267 | 1198 | 20 |
4 rows × 81 columns
house_df.dtypes
Id object
MSSubClass object
MSZoning object
LotFrontage object
LotArea object
...
MoSold object
YrSold object
SaleType object
SaleCondition object
SalePrice object
Length: 81, dtype: object
Welp, these aren’t the data types we want.¶
Let’s let pandas infer them to get the numeric types correct, then we’ll manually set the remaining object types to categories.
Afterwards, we’ll one-hot encode them
house_df = house_df.infer_objects()
house_df.dtypes
Id int64
MSSubClass int64
MSZoning object
LotFrontage float64
LotArea int64
...
MoSold int64
YrSold int64
SaleType object
SaleCondition object
SalePrice int64
Length: 81, dtype: object
So we still have categorical fields, let’s make sure they’re typed. TODO: change some of these to have the ordered attribute and see if that matters.
house_df[list(house_df.dtypes[house_df.dtypes == 'object'].index)] = house_df[list(house_df.dtypes[house_df.dtypes == 'object'].index)].astype('category')
Step 2) One-hot encoding¶
Let’s make sure that no column has more than 10 or so unique values before we one-hot-encode this
x_house_df = pd.DataFrame(house_df)
del x_house_df['SalePrice']
y_house_df = house_df.SalePrice
for colm in x_house_df.columns:
if x_house_df[colm].dtype == 'category':
if x_house_df[colm].nunique() >= 10:
print(f'{colm} {x_house_df[colm].nunique()}')
Neighborhood 25 Exterior1st 15 Exterior2nd 16
We’d better check these out, are these even categorical??
- Neighborhood: Checks out
- Exterior1st: Checks out
- Exterior2nd: Also…checks out.
print(f"Shape before adding dummies: {x_house_df.shape}")
for colm in x_house_df.columns:
if x_house_df[colm].dtype == 'category':
dummy = pd.get_dummies(x_house_df[colm], drop_first=True, prefix=colm)
x_house_df = pd.concat([x_house_df, dummy], axis=1).drop(colm, axis=1)
print(f"Shape after adding dummies: {x_house_df.shape}")
Shape before adding dummies: (1460, 80) Shape after adding dummies: (1460, 246)
81 features before adding dummies….
247 features after adding dummies. We made sure to remove the original as well. That pesky collinearity…
# This is gonna have to be much larger in size...
# sns.set(rc={"figure.figsize":(30*6, 15*4)})
# sns.heatmap(house_df.corr().abs(),annot=True,fmt='.1g')
# Let's be honest, this is too large to be useful
Step 3) Remove collinearity¶
For the first experiment, we created the rem_collinear_features() function to help remove collinearity. Let’s use that again. First, we must split this into x and y, then, in this order, pass: correlation_threshold, scoring, x_df, and y_df.
x_house_df = rem_collinear_features(0.4, f_regression, x_house_df, y_house_df)
Let’s see what we’re left with afterwards… before our shape would’ve been 1460×246 (if we exclude the SalePrice)
x_house_df.shape
(1460, 161)
x_train, x_test, y_train, y_test = train_test_split(x_house_df, y_house_df, shuffle=True, test_size=0.2, random_state = 11)
Let’s experiment!¶
lr2 = LinearRegression(n_jobs=-1)
lr2.fit(x_train, y_train)
LinearRegression(n_jobs=-1)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression(n_jobs=-1)
predictions = lr2.predict(x_test)
r2 = r2_score(y_test, predictions)
rmse = mean_squared_error(y_test, predictions, squared=False)
print(f'{r2} r^2 score')
print(f'{rmse} RMSE score')
0.7816534353344113 r^2 score 40278.60279969492 RMSE score
Our previous scores were…
0.73 r^2 score 44227 RMSE score
We’ve a higher r2 score and a lower RMSE!
Now:
0.78 r2 score
40278 RMSE score
Let’s Kaggle it!¶
To do this we must: impute, change the dtypes, one-hot-encode, and make sure we’ve the same columns
test_df = pd.read_csv('data/test.csv')
# Impute
imputer.fit(test_df)
test_df = pd.DataFrame(imputer.transform(test_df), columns = test_df.columns)
def missing_values(df):
df.shape
has_null = []
for col in df.columns:
if df[col].isnull().sum() > 0:
print(f'{df[col].isnull().sum()} null values in {col}')
#del test_df[colm]
has_null.append(col)
if df.isnull().sum().sum() == 0:
print("No missing values!")
else:
print(f"{df.isnull().sum().sum()} missing values")
return has_null
missing_values(test_df)
No missing values!
[]
test_df['Utilities'].unique()
array(['AllPub'], dtype=object)
# Change dtypes
test_df = test_df.infer_objects()
test_df[list(test_df.dtypes[test_df.dtypes == 'object'].index)] = test_df[list(test_df.dtypes[test_df.dtypes == 'O'].index)].astype('category')
# OHE
print(f"Shape before adding dummies: {test_df.shape}")
for colm in test_df.columns:
if test_df[colm].dtype not in(np.float64, np.int64):
dummy = pd.get_dummies(test_df[colm], drop_first=True, prefix=colm)
test_df = pd.concat([test_df, dummy], axis=1).drop(colm, axis=1)
print(f"Shape after adding dummies: {test_df.shape}")
Shape before adding dummies: (1459, 80) Shape after adding dummies: (1459, 228)
# Make sure we've the same columns
final_features = x_train.columns
test_df = pd.DataFrame(data=test_df, columns=list(final_features), )
missing_values(test_df)
1459 null values in Utilities_NoSeWa 1459 null values in Condition2_RRAn 1459 null values in Condition2_RRNn 1459 null values in HouseStyle_2.5Fin 1459 null values in RoofMatl_Membran 1459 null values in RoofMatl_Metal 1459 null values in RoofMatl_Roll 1459 null values in Exterior1st_ImStucc 1459 null values in Exterior1st_Stone 1459 null values in Exterior2nd_Other 1459 null values in Heating_OthW 16049 missing values
['Utilities_NoSeWa', 'Condition2_RRAn', 'Condition2_RRNn', 'HouseStyle_2.5Fin', 'RoofMatl_Membran', 'RoofMatl_Metal', 'RoofMatl_Roll', 'Exterior1st_ImStucc', 'Exterior1st_Stone', 'Exterior2nd_Other', 'Heating_OthW']
What in tarnation…
This test dataset doesn’t have all of the same unique categories in some columns as the training set.
We can’t use our model to predict wit these NA columns… unless… let’s try some imputer magic.
imputer.fit(x_house_df)
SimpleImputer(strategy='most_frequent')In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
SimpleImputer(strategy='most_frequent')
test_df = pd.DataFrame(imputer.transform(test_df), columns = test_df.columns)
BY GOLLY IT WORKED
to_kaggle_predictions_2 = pd.Series(data = lr2.predict(test_df), dtype=np.float32, name = 'SalePrice')
to_kaggle_predictions_2 = pd.concat([test_df['Id'],to_kaggle_predictions_2], axis=1)
to_kaggle_predictions_2['Id'] = to_kaggle_predictions_2['Id'].astype(np.int32)
to_kaggle_predictions_2.head()
| Id | SalePrice | |
|---|---|---|
| 0 | 1461 | 125123.546875 |
| 1 | 1462 | 99965.890625 |
| 2 | 1463 | 174925.500000 |
| 3 | 1464 | 220281.625000 |
| 4 | 1465 | 229191.562500 |
Let’s score up experiment #2!¶
to_kaggle_predictions_2.to_csv('submissions/to_kaggle_predictions_2.csv', index=False)
And we’ve done it with a score of Score: 0.47749
Even better!!!! Turns out scores closer to 0 are better.
I’m sure there is more improvement to be done. 3689 place now.
6) Experiment 3¶
Let’s just straight up factorize and impute it¶
For the next experiment, discuss what you try changing compared to the first experiment. For example, do you want to experiment with different features? Are you trying a different model? Then, talk about your results and how it changes from the previous experiment.
house_df = pd.read_csv('data/train.csv')
house_df = house_df.convert_dtypes()
We’re gonna have to factorize the train and test set together…
test_df = pd.read_csv('data/test.csv')
test_df = test_df.convert_dtypes()
One tiny note… let’s get rid of and seperate the ID columns before they get lost
del house_df['Id']
test_id_colm = test_df['Id']
del test_df['Id']
print(house_df.shape)
print(test_df.shape)
house_df = pd.concat([house_df, test_df])
(1460, 80) (1459, 79)
house_df[house_df.dtypes[house_df.dtypes == 'string'].index] = house_df[house_df.dtypes[house_df.dtypes == 'string'].index].apply(lambda x: pd.factorize(x)[0])
test_df = house_df.iloc[house_df.shape[0]-test_df.shape[0]:]
del test_df['SalePrice']
house_df = house_df.iloc[:house_df.shape[0]-test_df.shape[0]]
Seperate them and carry onwards!
print(house_df.shape)
print(test_df.shape)
(1460, 80) (1459, 79)
missing_values(house_df)
259 null values in LotFrontage 8 null values in MasVnrArea 81 null values in GarageYrBlt 348 missing values
['LotFrontage', 'MasVnrArea', 'GarageYrBlt']
imputer = SimpleImputer(missing_values=np.nan, strategy='mean') # also try strategy='most_frequent'
imputer.fit(house_df)
house_df = pd.DataFrame(imputer.transform(house_df), columns = house_df.columns)
We’re gonna split x and y early here
x_house_df = pd.DataFrame(house_df)
del x_house_df['SalePrice']
y_house_df = house_df.SalePrice
transformer = StandardScaler().fit(x_house_df)
x_house_df = pd.DataFrame(transformer.transform(x_house_df), columns = x_house_df.columns)
x_train, x_test, y_train, y_test = train_test_split(x_house_df, y_house_df, shuffle=True, test_size=0.2, random_state = 11)
lr3 = LinearRegression(n_jobs=-1)
lr3.fit(x_train, y_train)
LinearRegression(n_jobs=-1)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearRegression(n_jobs=-1)
predictions = lr3.predict(x_test)
r2 = r2_score(y_test, predictions)
rmse = mean_squared_error(y_test, predictions, squared=False)
print(f'{r2} r^2 score')
print(f'{rmse} RMSE score')
0.8505817661595017 r^2 score 33319.84824823273 RMSE score
Wow, that’s pretty nice.
Let’s get it on over to Kaggle
- Factorize (doen above)
- Impute
- Scale
- Predict!
# Impute
test_df['SalePrice'] = 0
test_df = pd.DataFrame(imputer.transform(test_df), columns = test_df.columns)
del test_df['SalePrice']
# Standard Scaler
test_df = pd.DataFrame(transformer.transform(test_df), columns = test_df.columns)
to_kaggle_predictions_3 = pd.Series(data = lr3.predict(test_df), dtype=np.float32, name = 'SalePrice')
to_kaggle_predictions_3 = pd.concat([test_id_colm,to_kaggle_predictions_3], axis=1)
to_kaggle_predictions_3['Id'] = to_kaggle_predictions_3['Id'].astype(np.int32)
to_kaggle_predictions_3.head()
| Id | SalePrice | |
|---|---|---|
| 0 | 1461 | 115585.132812 |
| 1 | 1462 | 210025.187500 |
| 2 | 1463 | 175096.203125 |
| 3 | 1464 | 205454.171875 |
| 4 | 1465 | 190090.031250 |
Okay last one!
to_kaggle_predictions_3.to_csv('submissions/to_kaggle_predictions_3.csv', index=False)
Score: 0.35858
3298 place
Better and better!
Experimental experiment using sklearn grid search¶
https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html
7) Impact Section¶
Discuss the possible impact of your project. This can be socially, ethically, etc. It cannot be something like “our project has no impact” or “our project has no negative impact.” Even the most well-intentioned projects could have a negative impact. We will not be checking for “right” or “wrong” answers, but showing your critical thinking.¶
Personally, I would hate for a perfect algorithm to be used to predict housing prices. I can only imagine that if there were more variables taken into account, including time and economic conditions, then this could get pretty darn close to accurate. If it could be used to predict future prices accurately, it could create a timeline in which people could invest in housing with 100% confidence. I personally think that this could reduce the overall populations home ownership proportion thus negatively impacting the overall proportion of families’ ability to aggregate generation wealth to pass on to their descendents.
On the flip side of this, if every ‘normal’ person could take advantage of this, the banks could be certain the loans they disperse would be safe. It all depends on the situation.
8) Conclusion¶
Discuss what you have learned from this project and through the different experiments. For example, did certain pre-processing steps help improve the model? Did you try using feature selection, and including/excluding certain features improve performance?¶
I’m thankful my results weren’t too accurate although it would’ve been very cool. I’ve learned I need to become more familiar with sklearns pipeline. I did end up finding a cool package called collinearity and becoming more familiar with sklearn. Pandas is really great for factorizing and adding dummies as well. Removing collinearity was a key component in some of my experiments, while standardizing data was key in my final one. I’d love to try our sklearns grid_search on this. I do intend to try out auto-sklearn on this as well. I’m currently trying to implement cuml (Nvidias drop-in replacement for sklearn) to run these faster and at parallel!
9) References¶
- https://www.kaggle.com/competitions/house-prices-advanced-regression-techniques/overview/evaluation
- http://www.amstat.org/publications/jse/v19n3/decock.pdf
- https://towardsdatascience.com/how-does-linear-regression-actually-work-3297021970dd
- https://towardsdatascience.com/introduction-to-machine-learning-algorithms-linear-regression-14c4e325882a
- https://github.com/gianlucamalato/collinearity
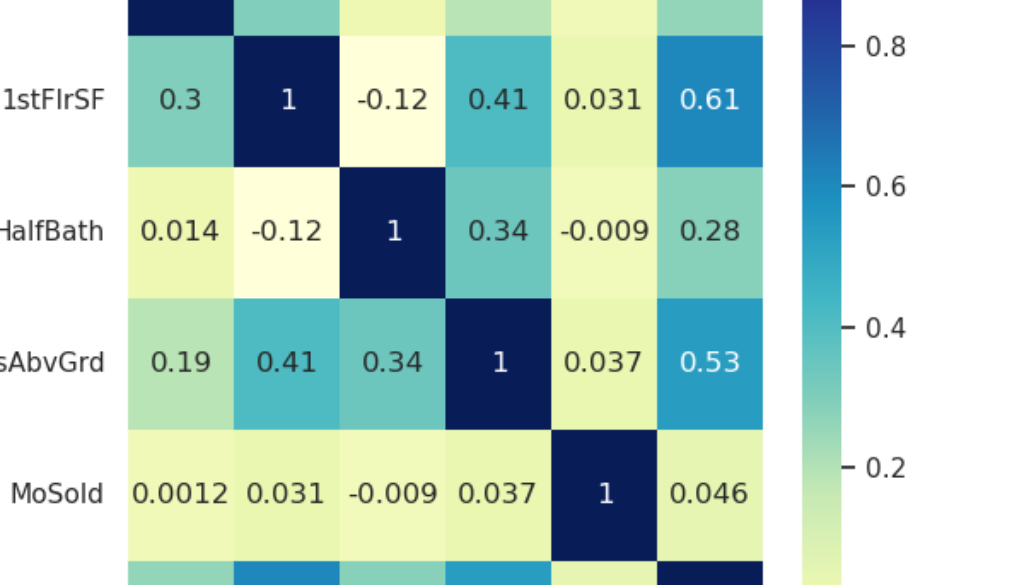
While we’re here… let’s use this to make an image for the website!
# TODO: Use 8 random values to create the correlation matrix
thumbnail_df = house_df[['LotArea','MoSold','TotRmsAbvGrd','SalePrice','1stFlrSF','HalfBath']]
# Maybe it's an awful idea...but the shape... and the fig size
thumbnail_size = thumbnail_df.shape[1]
sns.set(rc={"figure.figsize":(thumbnail_size, thumbnail_size)})
thumbnail = sns.heatmap(thumbnail_df.corr(), cmap="YlGnBu", annot=True, fmt='.2g')
Also to convert this to html: jupyter nbconvert –to html /path/to/example.ipynb –HTMLExporter.theme=dark from https://stackoverflow.com/questions/60894682/jupyter-notebook-exported-html-dark-color thanks nbconvert